Números 1 2 3 4 5 6 7 8
Vamos a definir cada nota con su número:
1 do
2 re
3 mi
4 fa
5 sol
6 la
7 si
8 do
Siendo el 8 (do) octava alta del 1 (do) .
Si mezclamos tres números: 1 3 5 ( do mi sol ) , hacemos un acorde triada , de tres notas.
Ahora mezclamos 8 números de tres en tres , ¿ cuántos acordes salen? .... muchisimos.... y mezclamos de cuatro en cuatro ( 1 3 5 7) , aún salen más.
Por eso digo yo siempre que la música es matemáticas.
En el piano numeremos las teclas blancas con números , y si nos fijamos arriba los número de las notas veremos cuales son en el piano.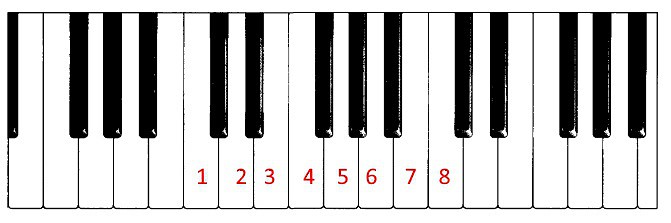

mezclamos tres números 1, 3, 5 do mi sol DO MAYOR
4, 6, 8 fa la do FA MAYOR
Todo en la música es matemáticas. Los dedos los nombramos, 1 2 3 4 5
Un medio tono lo nomnbramos 1/2t ...... Que es la distancia menor entre notas.....
En internet lo explican .... en la antigüedad ya decian que las matemáticas eran música.
Es común escuchar que “hay Matemática en la Música porque cuando se abre una partitura ésta está llena de numeritos”, es decir, de los números del compás y las digitaciones. Obviamente esta observación es muy simple. Se dice que hay Matemática en la Música, que la Música y la Matemática están muy relacionadas. Pero ¿hay Matemática en la Música? ¿Están relacionadas? ¿Qué relación existe entre la Música y la Matemática?
Hay desde luego similitudes innegables como que ambas tienen algo de mágico, son tan abstractas que parecen pertenecer a otro mundo y sin embargo tienen gran poder en este mundo, la música afecta al que escucha y las matemáticas tienen múltiples aplicaciones prácticas. Una parte de las matemáticas estudia los números, sus patrones y formas y estos elementos son inherentes a la ciencia, la composición y la ejecución de la música.
Leibniz describe a la Música como "un ejercicio inconsciente en la Aritmética". Esta afirmación quizás se podría justificar sobre la base de que el músico intérprete cuenta los tiempos del compás cuando comienza a estudiar una obra pero después de un tiempo de tocarla, ya no está contando conscientemente sino que deja fluir la magia de la Música. Sin embargo casi todos los "elementos externos" de la Música se definen numéricamente: 12 notas por octava; compás de 3/4, 7/8,...; 5 líneas en el pentagrama; n decibeles; semitono de raíz duodécima de dos; altura de 440 hz; lo horizontal y lo vertical en la textura musical; arriba y abajo en la escala; etc.
En tiempos de la antigua Grecia, la Música no sólo se consideró como una expresión artística de las Matemáticas sino que su estudio y análisis estuvo siempre ligado a la Teoría de los Números y a la Astrología. De hecho, para los griegos la teoría matemática de la música formaba parte de una teoría general conocida como la Armonía del Cosmo. Pitágoras y sus discípulos, Platón, Aristógenes, Aristóteles y Claudio Ptolomeo fueron algunos de los filósofos y astrólogos más relevantes que profundizaron en los intervalos musicales como fuente de nociones matemáticas y de importantes extrapolaciones científicas y cosmológica
En la Edad Media la Música estaba agrupada con la Aritmética, la Geometría y la Astronomía en el Cuadrivio. La Música no se consideraba un arte en el sentido moderno sino una ciencia aliada con la Matemática y la Física (la Acústica). Matemáticas un poco más elevadas se utilizaron en el cálculo de intervalos, el cual requería el uso de logaritmos, y los problemas del temperamento requerían del uso de fracciones continuas.
La música cambia su textura y carácter según el lugar y la época. Puede ser cristalina o densa, sentimental o explosiva. Por su parte, las matemáticas son directas, nunca alteran su carácter. La música se crea a partir de algo físico, instrumentos de todo tipo de materiales la producen. Las matemáticas son, sobre todo, abstracciones que no necesitan ni siquiera papel y lápiz. El mundo actual no podría concebirse sin ellas, ¿cómo haber llegado a la tecnología y a todos los inventos modernos sin las matemáticas?
La música está cargada de emociones, es alegre o triste, suave o agresiva, puede ser espiritual, estética, religiosa pero no podemos hablar de un teorema “triste” o de una demostración “agresiva”.
Tanto el matemático como el músico se encuentran ocupados resolviendo problemas o componiendo o interpretando, enseñando a alumnos sin detenerse a pensar que ambos están entregados a disciplinas que son paradigmas de lo abstracto.
Fuente Internet: IR A ARTÍCULO
No hay comentarios:
Publicar un comentario